重要的类 - Random

Random 类为您提供了简便的方法，可生成各种常用类型的随机值。

此页面概述了 Random 类及其使用该类编写脚本时的常见用法。有关 Random 类的每个成员的详尽参考以及有关它的更多技术细节，请参阅 Random 脚本参考。

请点击以下链接，了解这些有用方法的更多详细信息和示例。

简单的随机数

Random.value 返回一个随机浮点数，范围在 0.0 和 1.0 之间。一种常见的用法是将返回结果乘以所选范围，从而将其转换为介于 0 和该范围之间的数。

Random.Range 返回一个介于所提供的最小值和最大值之间的数。它返回整数或浮点数，具体取决于提供的最小值和最大值是整数还是浮点数。

圆形或球体内的随机点

Random.insideUnitCircle 返回一个半径为 1 的圆内随机选择的圆内点（同样，您可以将结果相乘，获得任意大小的圆内的随机点）。

Random.insideUnitSphere 返回一个半径为 1 的球内随机选择的球内点。

Random.onUnitSphere 返回一个半径为 1 的球上随机选择的球体的_球面_点。

其他类型的随机值

Unity 的 Random 类还提供了一些其他类型的随机值。

To generate a random rotation, use Random.rotation.

要生成一个随机颜色，使用 Random.ColorHSV。

从数组中选择一个随机项

随机选取一个数组元素归结为选择零和数组最大索引值（等于数组的长度减去 1）之间的一个随机整数。使用内置的 Random.Range 函数可以轻松实现：

 `var element = myArray[Random.Range(0, myArray.Length)];``

请注意，Random.Range 从包含第一个参数但不包含第二个参数的范围内返回一个值，因此在此处使用 myArray.Length 会得到正确的结果。

选择具有不同概率的项

有时需要随机选择项，但有些项比其他项被选中的几率更高。例如，NPC 在遇到玩家时可能会以几种不同的方式做出反应：

• 友好问候的几率为 50%
• 逃跑的几率为 25%
• 立即攻击的几率为 20%
• 提供金钱作为礼物的几率为 5%

可将这些不同的结果可视化为一张纸条，该纸条分成几个部分，每个部分占据纸条总长度的一个比例。占据的比例等于选择结果的概率。选择行为相当于沿着纸条的长度选择一个随机点（例如通过投掷飞镖），然后查看该点处于哪个部分。

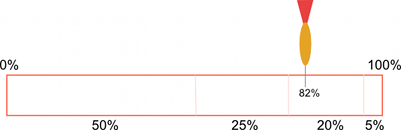
在脚本中，纸条实际上是一个浮点数组，其中的浮点数按顺序包含项的不同概率。随机点是通过将 Random.value 乘以数组中所有浮点数的总和得到的（这些数值不需要加起来等于 1；重点是不同值的相对大小）。要找到该点“位于”哪个数组元素，首先要检查它是否小于第一个元素中的值。如果是，则第一个元素便是选中的元素。否则，从该点值中减去第一个元素的值，然后将其与第二个元素进行比较，依此类推，直到找到正确的元素。在代码中表示为以下所示的内容：

float Choose (float[] probs) {

    float total = 0;

    foreach (float elem in probs) {
        total += elem;
    }

    float randomPoint = Random.value * total;

    for (int i= 0; i < probs.Length; i++) {
        if (randomPoint < probs[i]) {
            return i;
        }
        else {
            randomPoint -= probs[i];
        }
    }
    return probs.Length - 1;
}

请注意，最后的 return 语句是必要的，因为 Random.value 可以返回 1 的结果。在这种情况下，搜索将无法在任何地方找到随机点。将以下行

 `if (randomPoint < probs[i])`

…更改为“小于或等于”测试将避免额外的 return 语句，但也会允许偶尔选择某个项，即使其概率为零也是如此。

加权连续随机值

如果结果是不连续的，那么浮点数组方法会很有效，但在某些情况下希望产生更连续的结果；比如说，希望随机化一个宝箱中发现的金块数量，并希望能够出现 1 到 100 之间的任何数字，但让更小数字的概率更高。使用浮点数组方法来执行此算法将需要设置一个包含 100 个浮点数（即纸条上的部分）的数组，这是很不实用的方法；如果不局限于整数而是想要在该范围内的任何数字，则不可能使用这种方法。

一种适用于连续结果的更好方法是使用 AnimationCurve 将“原始”随机值转换为“加权”值；通过绘制不同的曲线形状，可产生不同的权重。代码编写起来也更简单：

float CurveWeightedRandom(AnimationCurve curve) {
    return curve.Evaluate(Random.value);
}

此算法从 Random.value 读取值来选择 0 到 1 之间的“原始”随机值。然后，该值传递给 curve.Evaluate()，在此处将其视为水平坐标，并返回曲线在该水平位置处的相应垂直坐标。曲线较平缓的部分被选取的几率较高，而较陡峭的部分被选取的几率较低。

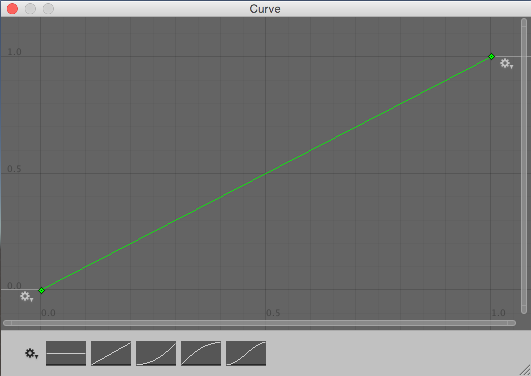
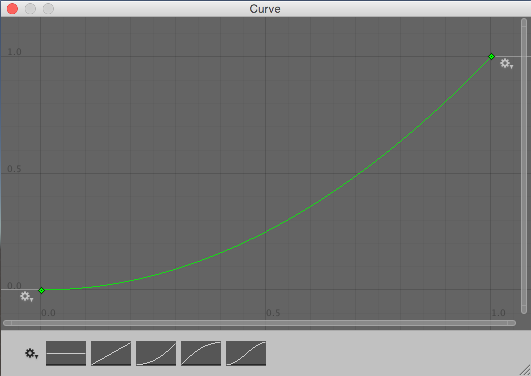
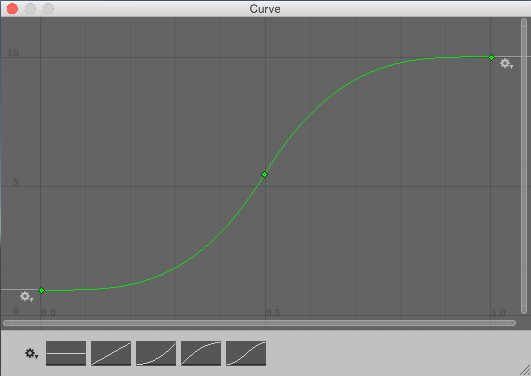
请注意，这些曲线并非概率论指南中可能介绍的概率分布曲线，而更像是反向累积概率曲线。

通过在一个脚本上定义 AnimationCurve 公共变量，可使用 Inspector 窗口直观查看和编辑曲线，而无需计算值。

这种方法会产生浮点数。如果要计算整数结果（例如，需要 82 个金块，而不是 82.1214 个金块），可将计算值传递给 Mathf.RoundToInt() 之类的函数。

列表洗牌

一种常见的游戏机制是从一组已知的项中进行选择，但让这些项以随机顺序到达。例如，一副纸牌通常需要洗牌，因此不会以可预测的顺序绘制。为了对数组中的项进行随机洗牌，可访问每个元素，然后将其与数组中位于随机索引处的另一个元素进行交换：

void Shuffle (int[] deck) {
    for (int i = 0; i < deck.Length; i++) {
        int temp = deck[i];
        int randomIndex = Random.Range(i, deck.Length);
        deck[i] = deck[randomIndex];
        deck[randomIndex] = temp;
    }
}

从一组无重复的项中选择

一种常见的任务是从一组中随机选取一些项，但不可多次选取同一项。例如，可能希望在一些随机生成点生成多个 NPC，但要确保每个点只生成一个 NPC。为实现此目的，可按顺序遍历这些项，随机决定是否将每一项添加到所选集合中。当访问每一项时，该项被选取的概率等于仍然需要的项数除以仍然可供选择的项数。

例如，假设有 10 个可用的生成点，但只能选择其中 5 个。选择第一项的概率为 5/10，即 0.5。如果选择了该项，那么第二项的概率将是 4/9，即 0.44（即仍然需要 4 项，还剩下 9 项可供选择）。但是，如果未选择第一项，那么第二项的概率将是 5/9，即 0.56（即仍然需要 5 项，还剩下 9 项可供选择）。这一直持续到该集合包含所需的 5 项为止。可使用如下所示的代码实现此算法：

Transform[] spawnPoints;

Transform[] ChooseSet (int numRequired) {
    Transform[] result = new Transform[numRequired];

    int numToChoose = numRequired;

    for (int numLeft = spawnPoints.Length; numLeft > 0; numLeft--) {

        float prob = (float)numToChoose/(float)numLeft;

        if (Random.value <= prob) {
            numToChoose--;
            result[numToChoose] = spawnPoints[numLeft - 1];

            if (numToChoose == 0) {
                break;
            }
        }
    }
    return result;
}

请注意，虽然选择是随机的，但所选集合中的项与原始数组中的项具有相同的顺序。如果要按顺序一次使用一项，那么这种排序可能使它们在一定程度上可预测，因此在使用之前可能需要对数组进行洗牌。

空间中的随机点

通过将 Vector3 的每个分量设置为 Random.value 返回的值可以选择立方体中的随机点：

` var randVec = Vector3(Random.value, Random.value, Random.value);`

这种算法可在边长为一个单位的立方体内部给出一个点。只需将矢量的 X、Y 和 Z 分量乘以期望的边长即可缩放该立方体。如果其中一个轴设置为零，则该点将始终位于单个平面内。例如，在“地面”上选取随机点通常需要随机设置 X 和 Z 分量并将 Y 分量设置为零。

当体积为球体时（即，希望从原点开始的给定半径内选取随机点时），可使用 Random.insideUnitSphere 乘以所需的半径：

` var randWithinRadius = Random.insideUnitSphere * radius;`

Note that if you set one of the resulting vector’s components to zero, you will not get a correct random point within a circle. Although the point is indeed random and lies within the right radius, the probability is heavily biased toward the center of the circle and so points will be spread very unevenly. You should use Random.insideUnitCircle for this task instead:-

 `var randWithinCircle = Random.insideUnitCircle * radius;`